电光Q开关.jpg)
技术文章
技术文章内容包括产品参数说明、原理说明，以及产品的应用等.
返回文章列表
相关内容
光学分辨率有极限吗？
分辨率
可以将密集的点区分为单个的点的能力。
分辨率极限（最大分辨率）
可识别为不同点的最小间距。光学分辨率极限的判定，最早是由物理学家恩斯特阿贝博士在1873年发现，可判定任何光学成像的分辨率理论极限。
凸透镜能将入射光聚焦到它的焦点上，但由于透镜口径有一定大小，光线透过时会由于波动特性会发生衍射，无法将光线聚成无限小的焦点上，而只会形成一定能量分布的光斑。中央是明亮的圆斑，周围有一组较弱的明暗相间的同心环状条纹，把其中以第一暗环为界限的中央亮斑称为艾里斑（Airy Disk）。图1为两个等光强的艾里斑从重叠到逐步分开的影像。
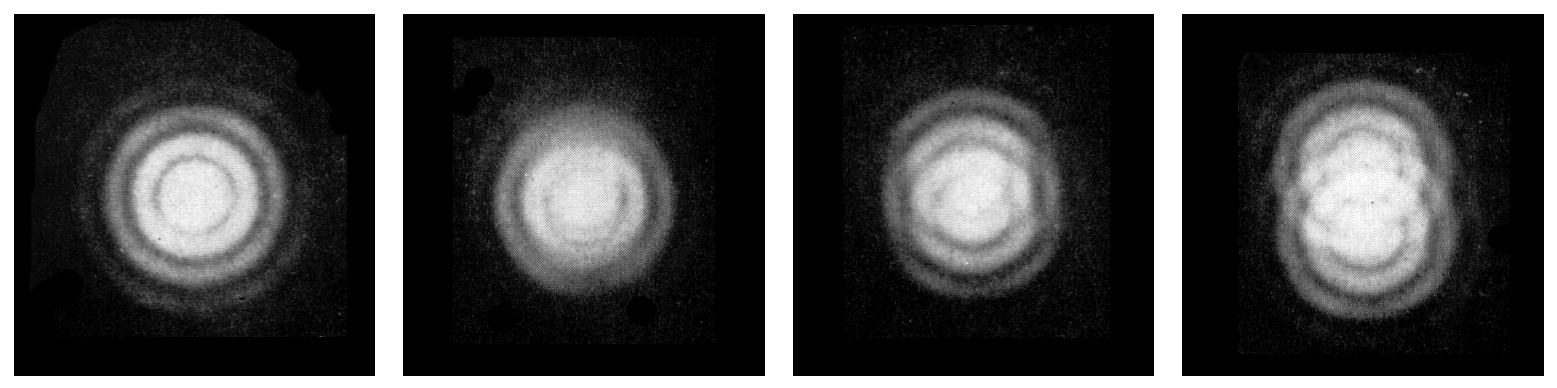
图1
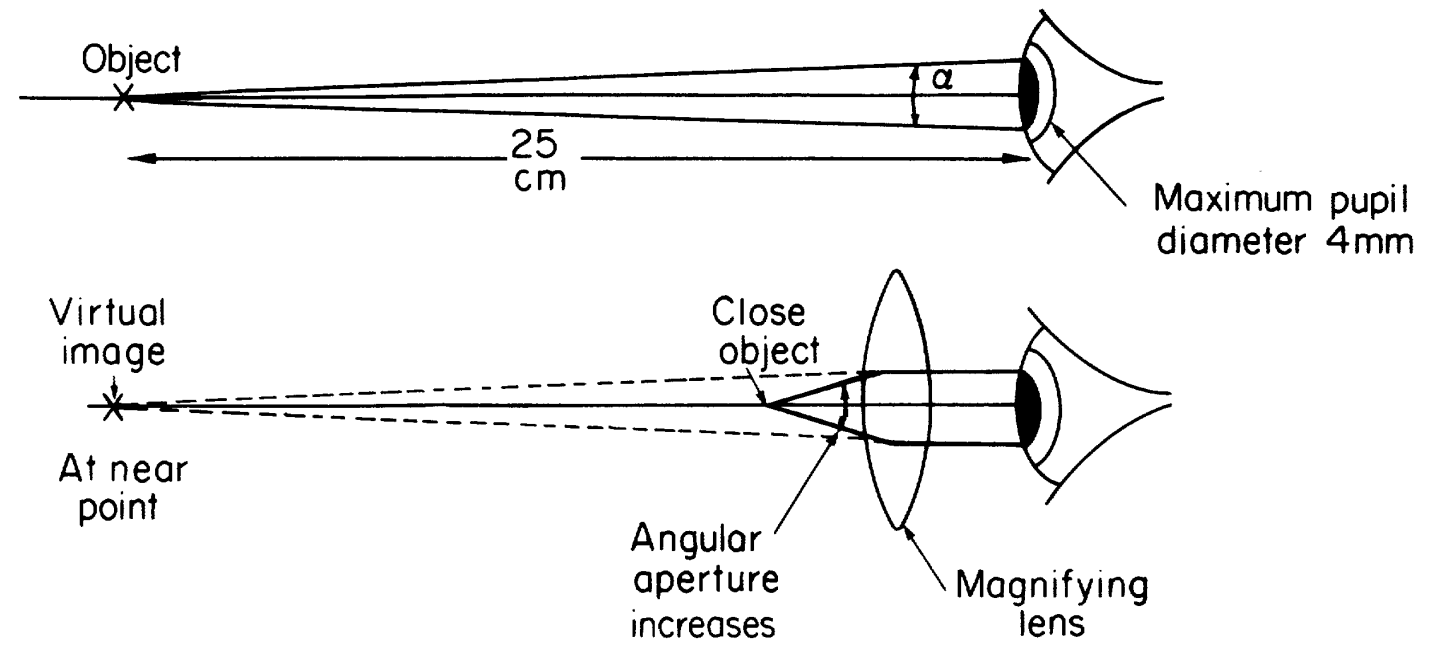
图2
从光的波动属性分析，物体细节对光的波动的反射才是物体被观察到的根本原因。通过发射波长等于或者小于物体大小的波，它被反射回观察者。而被观测物可以被观测到的最小尺度就是1/2波长，小于这个尺度被观测物将无法反射光波，从而无法被观测。
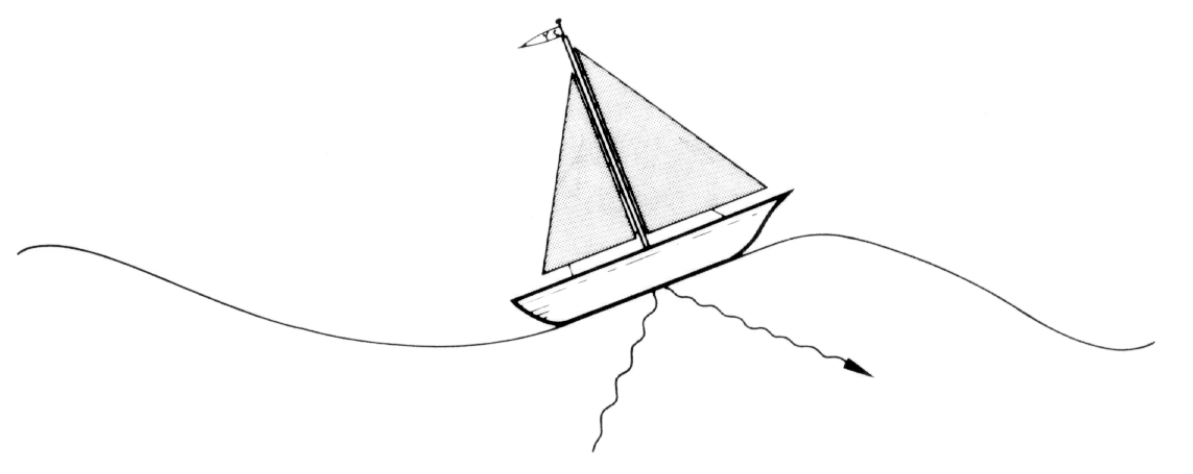
图3
最终，阿贝博士得出的阿贝简单判定(Abbe Simple Criterion)为：
式中λ为使用光线的波长值，n为光路中透镜对介质的折射率系数，α为入射光束与透镜光轴间的夹角。
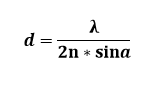
但是在实际应用中，被测物体不是一个点而是一系列物点的集合。每一个物点经过有限直径的透镜后，在像平面上都会产生文中开头提到的艾里斑，如果两个物点的艾里斑重叠到无法分辨，我们则认为这两个物点无法被分辨，图4中让两个等光强的非相干点像逐步分开，当两个点像中心间隔等于艾里斑的半径R，这样的艾里斑可以被认为是物点可以被分辨的最小尺寸，这种不同于阿贝简单判定的方式叫做瑞利判定（Rayleigh Criterion）。
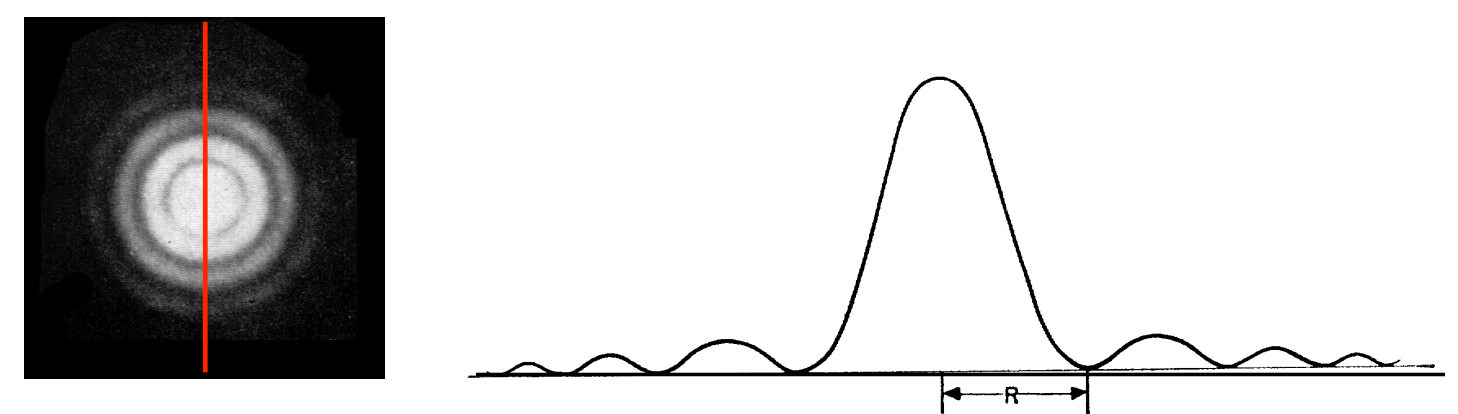
图4
那么我们来计算一下按照瑞利判定，可被分辨的艾里斑的半径（也就是可以被分辨的最小尺寸）与生成这个艾里斑的光波波长的关系。图5为原理示意图。
.png)
图5
中间演算过程涉及到冗长的傅里叶级数变换以及各种函数方程，最终计算结果为：
普通光学显微镜，为提高分辨率极限（使
一、减小λ值
可见光的波长范围：390nm～760nm，取可见光的波长为较短数值λ=400nm时（相当于紫色光），d≈200nm=0.2μm，这基本上可认为是一般光学显微镜的最高分辨能力了。
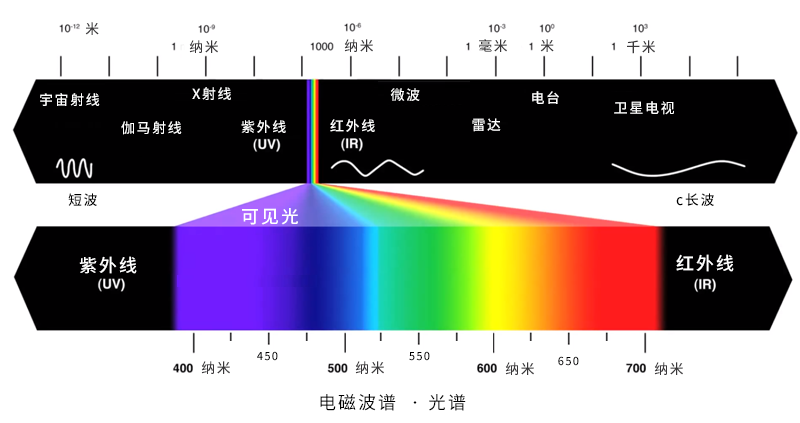
图6
在可见光波段想要获得更好的分辨率极限，显微镜系统在设计时就要尽量选用蓝紫光线作为照明光源。
二、增大n•sinα的值，这个值也被标为NA值（数值孔径）
选用折射率的更大的介质，以及增大孔径角有助于提高显微镜的分辨率。显微物镜上都会标识NA值（如图6中标识NA值为0.055），同等放大倍率的物镜，更大的数值孔径可以获得更好的分辨率。
.jpg)
图7
