DOE原理:光场调控的本质从守恒到重构
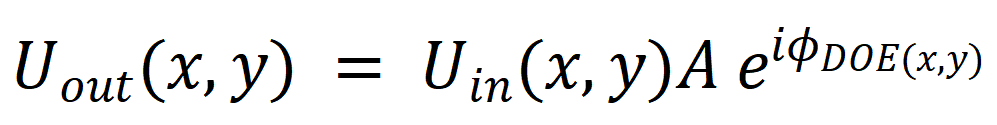
.png)
DOE算法:从目标光场到微结构的逆向设计
.png) 图2.典型的GS算法流程
图2.典型的GS算法流程平顶匀化DOE设计:多目标的均衡
.png) 图3. 方形匀化光斑效果
图3. 方形匀化光斑效果DOE的工业级案例:如何解决卡脖子难题
从DOE原理、智能设计算法,到工业落地场景与精密制造工艺,DOE以“无形之手”调控光场,打破传统光学边界,成为高端激光制造的核心“关键先生”,为相关领域注入创新动能。DOE技术迭代正加速,未来潜力无限。如需适配特定场景的选型方案,或想深挖相关技术细节,欢迎留言一起交流。
 微信扫码浏览
微信扫码浏览
DOE原理:光场调控的本质从守恒到重构
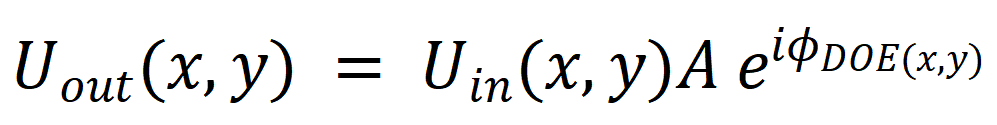
.png)
DOE算法:从目标光场到微结构的逆向设计
.png) 图2.典型的GS算法流程
图2.典型的GS算法流程平顶匀化DOE设计:多目标的均衡
.png) 图3. 方形匀化光斑效果
图3. 方形匀化光斑效果DOE的工业级案例:如何解决卡脖子难题
从DOE原理、智能设计算法,到工业落地场景与精密制造工艺,DOE以“无形之手”调控光场,打破传统光学边界,成为高端激光制造的核心“关键先生”,为相关领域注入创新动能。DOE技术迭代正加速,未来潜力无限。如需适配特定场景的选型方案,或想深挖相关技术细节,欢迎留言一起交流。